Channel decoding via deep learning (1)

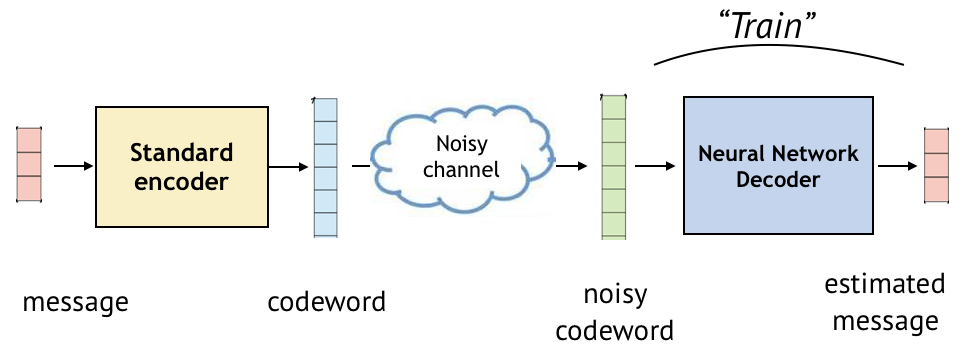
The first series of posts will cover applications of deep learning to channel coding, which is a basic building block of communication systems. An encoder maps messages (e.g., bit sequence) to codewords, typically of longer lengths. A decoder maps noisy codewords to the estimate of messages, as illustrated in a simplified figure below

desk

The design of channel codes is directly related to the reliability of communication systems; practical value of better codes is enormous. The design of codes is also theoretically challenging and interesting; it has been a major area of study in information theory and coding theory for several decades since Shannon’s 1948 seminal paper.

As a first step towards revolutionizing channel coding via deep learning, we ask the very first natural question. Can we learn optimal decoders solely from data?

Learning channel decoders

We fix the encoder as one of the standard encoders and learn the decoder for practical channels. When we fix the encoder, there’re many possible choices - and we choose sequential codes, such as convolutional codes and turbo codes. There are many reasons to it. First of all, these codes are practical. These codes are actually used for mobile communications as in 4G LTE, and satellite communications. Secondly, these codes achieve performance close to the fundamental limit, which is a very strong property. Lastly, the recurrent nature of sequential encoding process aligns very well with the recurrent neural network structure. Let me elaborate on this.

desk

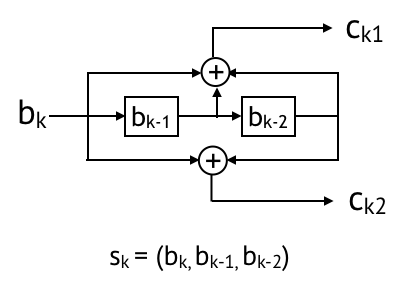
Sequential code

We’re going to show you an illusration of sequential code that maps a message sequence b to a codeword sequence c. We first take the first bit b₁, and update the state s₁, and the generate coded bits c₁ by looking at the state. Depending the rate of your code, c₁ can be of length 2 if it’s rate 1/2 or length 3 if it’s rate 1/3. And then you take the second bit b₂, then you update your state s₂ based on s₁ and b₂, and then geenrate coded bits c₂. And you do this recurrently, until you map the last bit b_K to the coded bit c_K.

Convolutional code

Convolutional code is an example of sequential codes. Here’s an example for a rate 1/2 convolutional code. Which maps bk to ck1 and ck2. The state is bk, bk-1, bk-2. Then the coded bits are convolution (or mod 2 sum) of the state bits.

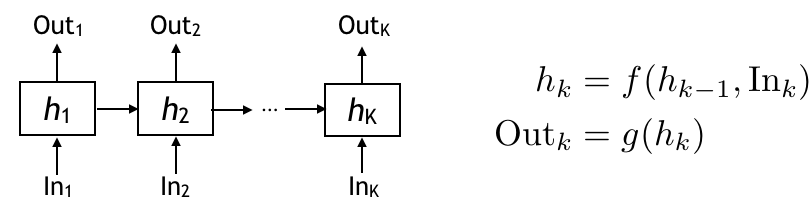
Recurrent Neural Network

Okay now let’s look at the Reccurent Neural Network architecture — (RNN in short) is a good neural architecture for sequential mappings with memory.

The way it works is there is a hidden state h evolving through time. The hidden state keeps some information about the current and all the past inputs. The hidden state is updated as a function of previous hidden state and the input at the time. Then the output is another function of the hidden state at time i.

In RNN, these f and g are some parametric functions. Depending on what parameteric functions you choose, the RNN can be a vanilla RNN, or LSTM, or GRU. And once you choose the parametric function, we then learn a good parameter through training.

So the RNN is a very natural fit to the sequential encoders.

Viterbi decoder

Now when it comes to decoding, for these sequential codes, there are well known decoders under AWGN settings - such as Viterbi and BCJR decoders …

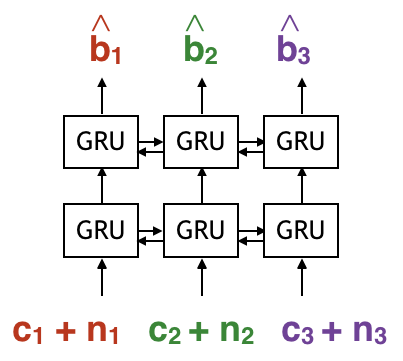
Modelling an RNN decoder

The first thing to do is to model the decoder as a neural network. We model the decoder as a bi-directional RNN because the encoder is sequential. We model the decoder as a Bi-directional RNN (which has forward pass and baackward pass) because we’d like the decoder to look at the whole received sequence to estimate a certain bit.

from keras import backend as K

import tensorflow as tf

from keras.layers import LSTM, GRU, SimpleRNN



block_length = 100 # Length of input message sequence  

code_rate = 2 # Two coded bits per one message bit

num_rx_layer = 2

num_hunit_rnn_rx = 50

noisy_codeword = Input(shape=(step_of_history, code_rate)) # size is (100, 2) - notation! 

x = noisy_codeword

for layer in range(num_rx_layer):

   x = Bidirectional(GRU(units=num_hunit_rnn_rx, 

          activation='tanh',

          return_sequences=True))(x)

   x = BatchNormalization()(x)

x = TimeDistributed(Dense(1, activation='sigmoid'))(x)

Predictions = x

model = Model(inputs=noisy_codeword, outputs=predictions)

Defining optimizer, loss, and evaluation metrics

optimizer= keras.optimizers.adam(lr=learning_rate,clipnorm=1.)



def errors(y_true, y_pred):

    myOtherTensor = K.not_equal(K.round(y_true), K.round(y_pred))

    return K.mean(tf.cast(myOtherTensor, tf.float32))



model.compile(optimizer=optimizer,loss='mean_squared_error', metrics=[errors])

print(model.summary())

Training

model.fit(x=train_tx, y=X_train, batch_size=train_batch_size,

          callbacks=[change_lr]

          epochs=num_epoch, validation_split=0.1)  # starts training

Results

GRAPH

References

Communication Algorithms via Deep Learning, Hyeji Kim, Yihan Jiang, Ranvir Rana, Sreeram Kannan, Sewoong Oh, Pramod Viswanath. ICLR 2018